South Asian Journal of Life Sciences
Research Article
Computational Study of Glucose-6-phosphate-dehydrogenase deficiencies using Molecular Dynamics Simulation
Hung Nguyen1, Thu Nguyen1, Ly Le1, 2*
1Life Science Laboratory, Institute for Computational Science and Technology, Ho Chi Minh City, Vietnam; 2School of Biotechnology, Ho Chi Minh International University, Vietnam National University, Vietnam.
Abstract | The aim of this work is to use molecular dynamics simulation to study the influence of mutated residues in interaction between G6P substrate-NADP+ coenzymes and Glucose-6-phosphate-dehydrogenase (G6PD) enzyme for wild type and three mutants (Vancouver, Wayne and Aachen mutants). The binding free energy (calculated by molecular mechanic Poisson-Boltzmann surface area (MM-PBSA) method) and hydrogen bond values between G6P substrate-NADP+ coenzymes and G6PD enzymes are identified as important in mutated residues to thermodynamic mechanism of G6PD enzyme in protecting the cells against oxidative stress and protective against malaria and this may assist further experimental study and strategies for rational design of new inhibitors.
Keywords | G6PD enzyme; G6P substrate-NADP+ coenzymes; wild type; Wayne, Aachen and Vancouver mutants; MM-PBSA method
Editor | Muhammad Nauman Zahid, Quality Operations Laboratory, University of Veterinary and Animal Sciences, Lahore, Pakistan.
Received | November 24, 2015; Accepted | May 22, 2016; Published | June 20, 2016
*Correspondence | Ly Le, School of Biotechnology, Ho Chi Minh International University, Vietnam National University, Vietnam; Email: ly.le@hcmiu.edu.vn
Citation | Nguyen H, Nguyen T, Le L (2016). Computational study of Glucose-6-phosphate-dehydrogenase deficiencies using molecular dynamics simulation. S. Asian J. Life Sci. 4(1): 32-39.
DOI | http://dx.doi.org/10.14737/journal.sajls/2016/4.1.32.39
ISSN | 2311–0589
Copyright © 2016 Nguyen et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
INTRODUCTION
Glucose-6-phosphate dehydrogenase (G6PD) is a X-chromosomally transmitted disorder of the erythrocyte, which is important in the control of oxidant stress in erythrocytes, the host cells for Plasmodium falciparum. Mutations in this enzyme produce X-linked deficiency states associated with protection against malaria. Some reports have proposed that heterozygous females with mosaic populations of normal and deficient erythrocytes (due to random X chromosome inactivation) have malaria resistance similar to or greater than hemizygous males with populations of uniformly deficient erythrocytes. These proposals are paradoxical, and they are not consistent with currently hypothesized mechanisms of protection (Aldiouma et al., 2007). There are approximately 400 million individuals suffering G6PD enzyme deficiency worldwide, being one of the most common inherited human enzyme defect (Nick et al., 2011; Miwa and Fujii, 1996). The disease was found to have originated from the abnormality of the G6PD gene located on the Xq28 chromosome, thereby leading to a decrease in the G6PD transcription or functional alteration (Bassam et al., 2012; Menziletoglu et al., 2011). Because G6PD plays a crucial role in protecting red blood cells from the harmful influence of reactive oxygen species (ROS), disadvantageous mutations in the G6PD gene result in ROS accumulation, ultimately leading to hemolytic anemia (Cappellini and Fiorelli, 2008). Over 200 G6PD mutations have been found with different distributions in populations worldwide though several mutations were found to have higher frequency compared with others (Bassam et al., 2012). One of G6PD deficiency consequences is the loss of function of the demerit G6PD gene induced by disadvantageous mutations.
The G6PD enzyme is responsible for converting glucose-6-phosphate (G6P) into 6-phosphoglucono-δ-lactone in the pentose phosphate pathway and producing
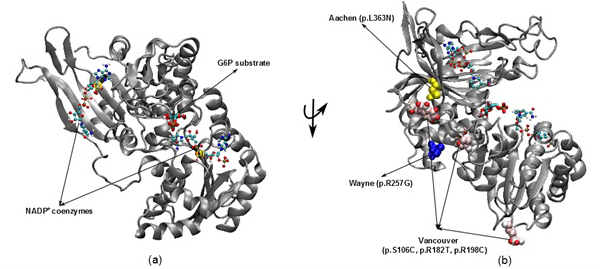
Figure 1: The illustration was shown the G6PD enzyme with two NADP+ coenzymes entry from 2BH9 and G6P substrate entry from 2BHL for wild type (a) and three mutants including Vancouver (p.S106C, p.R182T and p. R198C), Wayne (p.R257G) and Aachen (p.L363N) (b)
nicotinamide adenine dinucleotide phosphate (NADPH) (McMullin, 1999). Since the main role of red blood cells is to carry oxygen, they are always at high risk of damage from oxidizing free radicals except for the protective effect of G6PD/NADPH/glutathione (Beutler, 1994). G6PD enzyme protects the blood cells against oxidative damage by maintaining the level of the NADPH. The NADPH in turn maintains the supply of reduced glutathione in the cells that is used to neutralize reactive oxygen species (Sikka et al., 2011). Previous study on G6PD variants found six German Ancestral G6PD variants (Roman and Swindells, 2011) of which, three particular variants (Vancouver, Aachen and Wayne) were found to locate within the active site region (Figure 1). Specifically, two of the three mutated residues in the Vancouver variant (p.R198C and p.R182T), Aachen variant with p.L363N and Wayne variant with p.R257G are near of the substrate-binding pocket of G6P substrate and the second NADP+(2) or in the interface between the monomers, which is not to the first NADP+(1). These mutations were suggested to have involvement in the binding of G6P and NADP+ to G6PD enzyme and the loss of G6PD function. The recent studies have focused on the effects of G6P substrate and NADP+ coenzymes on G6PD’s surface in wild type and mutated variants structures (Kiani et al., 2007).
In this study, we employed molecular dynamics simulation to investigate the dynamic properties of wild type and three mutants of the G6PD enzyme. Specially, we focused on the alterations upon interaction between G6PD active site regional mutations and G6P substrate-NADP+ coenzymes, along with identifying amino acid residues that play important roles in G6P substrate and NADP+ coenzymes. Binding free energy between the G6P substrate-NADP+ coenzymes and G6PD enzyme for wild type and the mutants (Vancouver, Aachen and Wayne mutants) were also calculated to reveal the basic changes that lead to G6PD deficiency at molecular level.
MATERIAL AND METHODS
Materials
The 3D structures of wild type with NADP+ coenzymes and G6P substrate were taken from PDB database with PDB entry 2BH9 and 2BHL (Kiani et al., 2007), respectively. Then, the superimposed technique in Visual Molecular Dynamics (VMD) software (Humphrey et al., 1996) was applied to build the complex structure for G6PD enzyme from two 3D structures (2BH9 and 2BHL). The structures of three German ancestral variants were prepared with their corresponding mutations (p.S106C, p.R182T and p.R198C in Vancouver variant, p.L363N in Aachen variant and p.R257G in Wayne variant). The variants were built from wild type structure via using tools in VMD (Figure 1).
Molecular Dynamics Simulations
All simulations were performed with GROMACS 4.5.5 package (Berk et al., 2008) using GROMOS96 43a1 force field (Gunsteren et al., 1996). During the simulation process, the periodic boundary conditions were set at 1.4 nm cut-off for electrostatic and van der Waals (vdW) interactions, respectively. The electrostatic interaction was calculated using particle-mesh Ewald summation method (Tom et al., 1993). The complex structures were solvated in SPC/E water model (Pekka and Nilsson, 2001).
Water molecules were replaced by Na+ and Cl- ions inside the box to neutralize electric charges for simulation complexes. The equilibration process was performed coupling with temperature and pressure conditions. Constant temperature 300 K was enforced using Berendsen algorithm (Berendsen et al., 1984) under 1.5 ns for constant volume and temperature (NVT). The Parrinello-Rahman pressure coupling (Parrinello and Rahman, 1981) in 2 ns constant pressure and temperature (NPT) run at 1 bar constant pressure. All bond lengths were constrained with the linear constraint solver LINCS (Berk et al., 1997) as implemented in GROMACS software. Molecular dynamics simulations allowed integrating the equations of motion with time step of 1 fs in the leap frog algorithm (Hockney et al., 1974).
Binding Free Energy
Binding free energies between G6P substrate-NADP+ coenzymes and G6PD enzymes were calculated by the Molecular Mechanics/Poisson-Boltzmann Surface Area (MM-PBSA) method (Wang et al., 2001; Nguyen and Le, 2015). The binding free energy calculation is defined by:
ΔG = Gcomplex – Gfree-protein – Gfree-ligand (1)
The free energy of each molecule in the MM-PBSA is given by:
G = Emm + Gsolvation –T (2)
In which,
the Emm was calculated for each snapshot that no cutoffs:
Emm = Ebond+ Eangle+ Eelec+ EvdW + Etorsion (3)
Here,
the electrostatic (Eelec) and vdW (EvdW) interactions are computed by Gromacs software used in MD simulations.
The Gsolvation was approximated by contributing of the sum of electrostatic and nonpolar:
Gsolvation = GPB + Gsur (4)
And the GPB was determined using the continuum solvent approximation (Sharp and Honig, 1990). Which was the change of electrostatic interaction by transferring solute in a continuum medium from a low solute dielectric constant (ε = 2) to a higher one with water without salt (ε = 78.45). The APBS package (Baker et al., 2001) was implemented for solution of the corresponding to linear Poisson-Boltzmann equation. And the nonpolar solvation term Gsur was approximated as linearly dependent on the solvent accessible method (Shrake and Rupley, 1973) in the APBS package:
Gsur = γSASA + β (5)
Where;
γ = 0.0072 (kcal/mol).Å2 and β = 0.
The entropy was estimated from the average of three snapshots randomly taken from MD simulations. The simulation structures were minimized with no cutoff for non-bonded interactions by using the conjugate gradient and low memory Broyden - Fletcher - Goldfarb - Shanno method (Sitkoff et al., 1994) until the maximum fore was smaller than 10-6 kJ/(mol.nm). The conformational entropy of the solute S was estimated by normal mode analysis by diagonalizing the mass weighted Hessian matrix (Shanno, 1970):
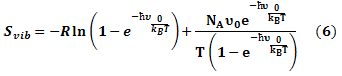
Where;
Svib is the vibrational entropy, ћ is Plank’s constant, υ0 is the frequency of the normal mode, kB is the Boltzmann constant, T is 300 K, and NA is Avogadro’s number. We used snapshots collected in the equilibrium of each system to calculate other terms of binding free energy.
Analyzing Data
The root mean square deviation (RMSD) is calculated to measure the deviation of structure from the initial configuration. The bond stretching distribution is used to reveal the bonding between the mutated residues and its surrounding residues. The hydrogen bond is distance between proton donor (D) and proton acceptor (A), which is less than 0.35 nm and the angle H-D-A is also less than 300 (Nguyen et al., 2011; Nguyen et al., 2015). All of the analyzing was using the tools in Gromacs software to analyze.
RESULTS AND DISCUSSION
Binding Sites of NADP+ Coenzymes and G6P Substrate
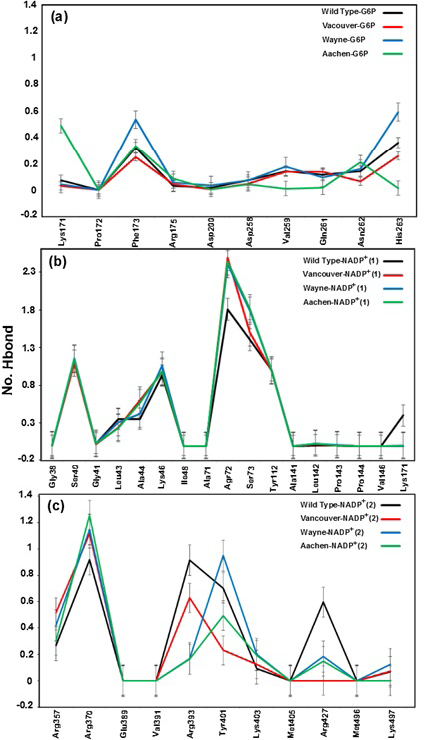
Binding motifs of G6PD enzyme revealed that the enzyme family possesses three binding sites: two of NADP+ coenzymes (NADP+(1) and NADP+(2)) and one of G6P substrate. The G6P substrate is closer to NADP+(1) than that to NADP+(2) (Kiani et al., 2007). The Figure 2 showed the binding sites of G6P substrate (Figure 2a), NADP+(1) and NADP+(2) coenzymes (Figure 2b), which showed all hydrogen bond and hydrophobic interactions between G6P substrate-NADP+ coenzymes and G6PD enzyme by using LigPlot software (Roman and Swindells, 2011; Wallace et al., 1995). This analysis reveals that G6PD requires two NADP+ molecules as coenzymes and each has a distinct binding pocket. In detail, there were two residues formed hydrogen bonds with G6P and NADP+(2) and six residues formed hydrogen bonds with NADP+(1).
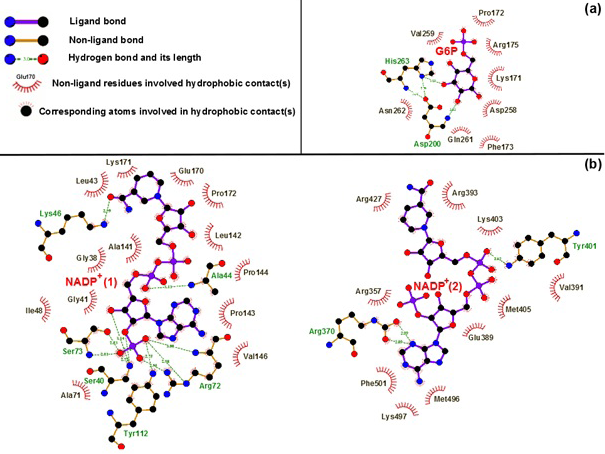
Figure 2:Hydrogen bond and hydrophobic interactions between G6P substrate (a), two NADP+ coenzymes (b) and the G6PD enzyme Which was prepared by LigPlot software
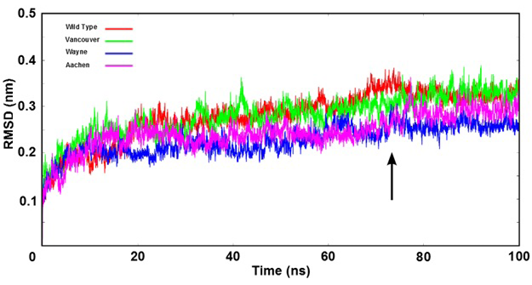
Figure 3: The root mean square deviation (RMSD) of backbone of the G6PD enzymes were shown as time function. Here, the arrow indicates that all systems were reached the equilibration state after 75 ns
Stability of Simulation Systems
The stability of wild type and three mutations of G6PD enzyme was analyzed using the root mean square deviation (RMSD) values. The RMSD’s values were plotted as a function of time (Figure 3). All systems reached the equilibration state after 75 ns with RMSD’s values were fluctuated approximately from 0.25 nm to 0.35 nm. And trajectories of the systems were extracted from equilibrium state for stability analysis and subsequent binding free energy calculation.
The Effect of Reference Mutations on G6PD Enzyme Activity
The Figure 4 shows bond stretching distribution of the wild type and mutants as a function of bond length in order to describe the change of bonding network between mutated residues and its neighboring residues in the G6PD enzymes. In further analysis showed that the effect of mutated residues to its neighboring residues in G6PD enzyme did change the bonding between G6P substrate-NADP+ coenzymes and G6PD enzymes. The Figure 4a reveals bond stretching distribution of three mutated residues (p.S106C, p.R182T and p.R198C) of Vancouver and the residues (S106, R182 and R198) of wild type with its neighboring residues. We found that all of three peaks overlapped, and which just fluctuated from 0.09 nm to 0.16 nm. The height of peaks decreased when the bond length values increased. This result showed that bond stretching distribution of Vancouver and wild type may have
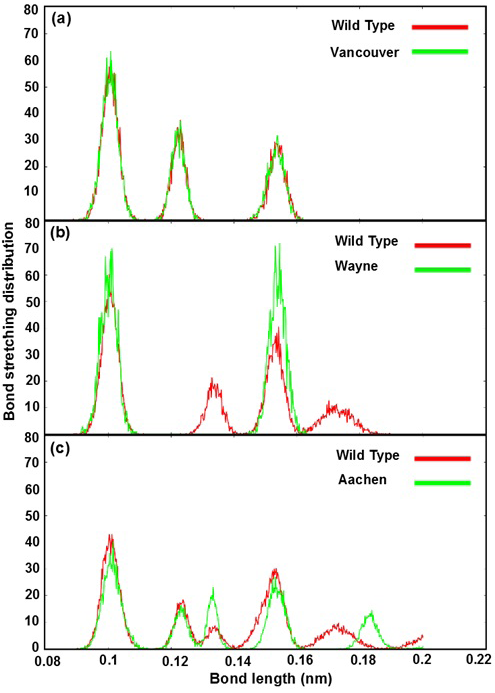
Figure 4: Bond stretching distribution revealed the bonding between the mutated residues and its surrounding residues as bond length function
a), b) and c) were illustrated the bonding between S106, R182, R198 residues of wild type and p.S106C, p.R182T, p.R198C mutated residues of Vancouver variant; between R257 residue of wild type and p.R257G mutated residue of Wayne variant and between L363 residue of wild type and p.L363N mutated residue of Aachen variant
insignificant effect on G6PD enzyme activity. Which was found the mutated residues also contribute to the bonding formation between G6P substrate-NADP+ coenzymes and binding site residues but the differences were not significant. The Figure 4b describe the differences of bond stretching distribution between p.R257G mutated residue of Wayne and R257 residue of wild type with its neighboring residues. The bond stretching distribution of Wayne has two peaks meanwhile wild type has four peaks. However, the height of two peaks in Wayne was higher than that in wild type and the bond length of the residues fluctuated from 0.09 nm to 0.19 nm. Here, the loss of peak number of bond stretching distribution in Wayne have led to the significant changing for the binding between G6P substrate-NADP+ coenzymes and binding site residues. The Figure 4c illustrates bond stretching distribution of p.L363N mutated residue of Aachen and L363 residue of wild type with its neighboring residues. There are five peaks for both systems and bond length fluctuated from 0.09 nm to 0.2 nm. Two first peaks of them overlapped in scope from 0.09 nm to 0.13 nm and three remaining were completely different. The differences among three remaining peaks were caused by the influence of p.L363N mutated residue in bonding to surrounding residues.
Based on the bond stretching distribution values, we found that the bonding of mutated residues to surrounding residues lead to the loose of hydrogen bond between G6P substrate-NADP+ coenzymes and G6PD enzyme in wild type and the mutants, which will be described in detail as below.
a), b) and c) were corresponding to hydrogen bonds between G6P substrate, NADP+ (1) and NADP+ (2) coenzymes and the G6PD enzymes, respectively
Hydrogen Bond between G6P Substrate-NADP+ Coenzymes and G6PD Enzymes
Hydrogen bonds mainly contribute to the electrostatic energy from MM-PBSA results, which play a key role in the interaction between ligands and protein. As shown in Figure 5, the hydrogen bond values between G6P substrate-NADP+ coenzymes and G6PD enzymes display the differences in hydrogen bond forming between G6PD enzymes and G6P substrate-NADP+ coenzymes for wild type and three mutants. The Figure 5a shows hydrogen bonds between the G6P substrate and G6PD enzyme for wild type and three mutants. Here, there are not many differences of hydrogen bonds among wild type, Vancouver and Wayne whereas Aachen has the significant changes including the loss of hydrogen bond of Val259, Gln261 and His263. Unlike the situation of wild type, Wayne and Vancouver variants, the hydrogen bonds of Lys171 residue of Aachen variant did not lose. In Figure 5b, the loss of the hydrogen bonds between NADP+(1) coenzyme and Lys171 residue in three mutants was accompanied by interacting between mutated residues and the binding site residues. The Figure 5c shows hydrogen bond between NADP+ (2) coenzyme and the binding site residues for wild type and three mutations. The hydrogen bond between Arg427 residue of Vancouver and NADP+ (2) coenzyme was completely broken due to influence of p.S106C, p.R182T and p.R198C mutated residues, and which is also decreased comparing with wild type in two remaining mutations.
With gained results from Figure 5, we found that the Lys171 residue depends not only on binding site of G6P substrate but also binding site of NADP+(1) coenzyme. And the mutated residues in the mutants have a major role in inhibiting the hydrogen bonding between G6PD enzymes and G6P substrate-NADP+ coenzymes.
Binding Free Energies
In order to gain insights into the contribution of each energy component to ligands’ potency, the binding free energies between G6P substrate-NADP+ coenzymes and G6PD enzyme for wild type and three mutants were estimated using molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) method. The binding free energy between G6P substrate-NADP+ coenzymes and G6PD enzyme by MM-PBSA method was calculated in the final 25 ns production run of 100 ns simulation (Table 1).
As shown in Table 1, the electrostatic interaction and polar solvation were the key factors for the difference between wild type and the mutations and in calculating the binding free energy, which was compensated together. The electrostatic interaction of wild type (∆Eelec = 116.01 (kcal/mol)) was larger than 0 (kcal/mol) whereas the electrostatic interaction of the mutants are smaller than 0 (kcal/mol) corresponding for Vancouver (∆Eelec = -19.32 (kcal/mol)), Wayne (∆Eelec = -8.68 (kcal/mol)) and Aachen (∆Eelec = -19.52 (kcal/mol)). Contrary with electrostatic interaction, the polar solvation of wild type (∆Gpolar= -133.75 (kcal/mol)) was smaller than 0 (kcal/mol) while the polar solvation of Vancouver (∆Gpolar = 24.73 (kcal/mol)), Wayne (∆Gpolar = 26.17 (kcal/mol)) and Aachen (∆Gpolar = 21.12 (kcal/mol)) were larger than 0 (kcal/mol). Additionally, Table 1 was also shown the vdW interactions was fluctuated between -15.01 (kcal/mol) and -29.24 (kcal/mol) and the apolar solvation was fluctuated between -3.21 (kcal/mol) and -10.12 (kcal/mol). They were importantly contributed for the difference in calculating the binding free energy but if being the difference of wild type and the mutations then which was not significant. The entropy contribution (-T∆S) of wild type was 4.35 (kcal/mol) meanwhile the -T∆S of three mutants were corresponding to 17.65 (kcal/mol) for Vancouver, 6.32 (kcal/mol) for Wayne and 17.11 (kcal/mol) for Aachen. Not much difference among the entropy values of wild type and three mutants was observed. Finally, the binding free energy revealing for wild type (∆GMM-PBSA = -38.62 (kcal/mol)) was smaller than the mutants (the ∆GMM-PBSA values were corresponding to -7.44 (kcal/mol) for Vancouver, -1.32 (kcal/mol) for Wayne and -13.74 (kcal/mol) for Aachen variants). This means the binding between G6P substrate-NADP+ coenzymes and G6PD enzyme in wild type have tended durable binding meanwhile three mutants have tended less durable binding better or the wild type structure was more stable than the mutants. These results were demonstrated for the effects and important role of mutated residues in the mutants, which completely changed initial thermodynamic property of wild type structure. These mutations were causing resistance to malaria as previously mentioned. This detection was interesting to discover important role of mutated variants in protecting the cells against oxidative stress and its mutations resulted in changing the catalytic activity of the G6PD enzyme and protective against malaria.
Table 1: The Binding free energies calculated by MM-PBSA method (kcal/mol)
|
∆Eelec |
∆EvdW |
∆Gpolar |
∆Gapolar |
-T∆S |
∆GMM-PBSA |
|
|
Wild type |
116.01±21.12 |
-17.02±5.81 |
-133.75±33.31 |
-8.21±6.01 |
4.35±1.33 |
-38.62±12.06 |
|
Vancouver |
-19.32±11.43 |
-27.13±9.22 |
24.73±8.41 |
-3.37±1.01 |
17.65±4.17 |
-7.44±2.07 |
|
Wayne |
-8.68±6.27 |
-15.01±5.55 |
26.17±7.36 |
-10.12±5.33 |
6.32±4.03 |
-1.32±1.03 |
|
Aachen |
-19.52±9.71 |
-29.24±12.91 |
21.12±9.34 |
-3.21±0.92 |
17.11±3.31 |
-13.74±4.14 |
CONCLUSIONS
The MD simulation was employed to study the binding relationship between G6P substrate-NADP+ coenzymes and G6PD enzyme for wild type and three mutants, we have obtained several significant results: (i) The interaction between the mutated residues and its neighboring residues in G6PD enzymes have changed the initial characteristics of G6PD enzyme and reduced the hydrogen bond number between the G6P substrate-NADP+ coenzymes and G6PD enzyme which did change most of the thermodynamic mechanism as well as initial properties of G6PD enzyme. (ii) The mutated residues were found to cause the differences of electrostatic interaction and polar solvation values between wild type and the mutants, which lead to the loss of binding free energy between G6P substrate-NADP+ coenzymes and G6PD enzyme in the mutants. (iii) The research demonstrated that the mutants have a key role in protecting the cells against oxidative stress and changing the catalytic activity of the G6PD enzyme as well as its protective against malaria.
ACKNOWLEDGEMENTS
The work was supported by the Department of Science and Technology at Ho Chi Minh City, Vietnam. The computing resources and support provided by the University of Oklahoma Supercomputing Center for Education & Research are gratefully acknowledged.
CONFLICT OF INTEREST
The authors declare that they have no competing interest.
Authors’ contribution
Hung Nguyen collected and analysed the data. and drafted the manuscript. Thu Nguyen analysed the data. Ly Le participated in the design of the study and revised the manuscript.
REFERENCES