Research Article

 

Principal Component Analysis for Body Weight Prediction of Corriedale Ewes from Southern Peru

 

Ali William Canaza-Cayo 1*, Rodrigo Reis Mota2, Fernando Amarilho-Silveira3, Darlene Ana Souza Duarte2, Jaime Araujo Cobuci3

1Faculty of Agrarian Sciences, Agronomic Engineering School, National University of Altiplano, (051) 599430 Av. Floral Nº 1153, Puno, Peru; 2CDCB - Council on Dairy Cattle Breeding 4201 Northview Drive, One Town Centre, Suite 302 Bowie, MD 20716, United States of America; 3Animal Science Department, Federal University of Rio Grande do Sul, Porto Alegre, Brazil.

 

Received | July 21, 2021; Accepted | August 08, 2021; Published | October 01, 2021

*Correspondence | Ali William Canaza-Cayo, Faculty of Agrarian Sciences, Agronomic Engineering School, National University of Altiplano, (051) 599430 Av. Floral Nº 1153, Puno, Peru; Email: alicanaza@unap.edu.pe

Citation | Canaza-Cayo AW, Mota RR, Amarilho-Silveira F, Duarte DAS, Cobuct JA (2021). Principal component analysis for body weight prediction of corriedale ewes from southern peru. J. Anim. Health Prod. 9(4): 417-424.

DOI | http://dx.doi.org/10.17582/journal.jahp/2021/9.4.417.424

ISSN | 2308-2801

Copyright © 2021 Canaza-Cayo et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

 

Introduction

 

The sheep population in Peru is estimated to ~9.5 million animals. A total of 81% from this value comprised the Criollo breed. This breed is usually raised by peasant communities. In addition, the Corriedale breed represents 11.4% of the total population whereas other breeds 7.6% (INEI, 2012). Unlike Criollo, Corriedale animals are raised by communal cooperatives and private farmers. This breed is dual-purpose (wool and meat) and is widespread with major herds in Puno, Pasco, Cusco and Junín regions of Peru. These animals are characterized by good body development, and their dense fleece is medium-fine and high yielding. However, the sheep population in Peru has decreased overtime (INEI, 2012). The primary reasons are the use of grasslands for field crop cultivation, low production levels, and insufficient income levels in the present production systems. This thereby generates a deficit of meat production (Iñiguez et al., 2011; Williams and Anderson, 2020).

 

An alternative to this situation is an efficient herd management through periodical evaluation of production parameters (e.g., body weight and composition, measurements). Body weight is an important parameter for to assess the general condition of an animal, to increase meat production via selection, for feeding management, health care, to determine the end of fattening period and so on (Kunene et al., 2009; Yilmaz et al., 2013). However, given the importance of sheep farming for the country and the scarcity of studies on this topic, it is necessary to develop a way to estimate body weight, composition and other measurements in a simpler and less biased manner.

 

A feasible alternative would be to use body measurements, an indirect, fast, and low-cost method. Prediction of sheep body weights from body measurements has been reported by several authors for different breeds (Atta and El khidir, 2004; Riva et al., 2004; Silva et al., 2006; Sowande and Sobola, 2008; Kunene et al., 2009). It has been observed, however, that different models might be needed to predict body weight for different environmental conditions, body condition score and breeds (Enevoldsen and Kristensen, 1997).

 

This is due to the different biological relationship that exists among linear body measurements (Yakubu and Ayoade, 2009), and may lead to collinearity (Akinsola et al., 2014). Thus, principal component analysis (PCA), a multivariate technique, can be used with much success when morphological traits present multicollinearity (Mavule et al., 2013). PCA uses orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components (Jolliffe, 2002). PCA of body measurements has been used as a tool in breed description and characterization of different sheep breeds (Riva et al., 2004; Cerqueira et al., 2011; Legaz et al., 2011; Silva et al., 2013) as well as to predict body weight (Mavule et al., 2013; Eyduran et al., 2013).

 

To the best of our knowledge, there are no studies, which has developed linear regression equations for prediction of the body weights using principal component scores in Corriedale breed raised in extensive systems in Peru. Therefore, our objective was to estimate the relationship between body measurements and body weight as well as to determine the best model for investigate body weight prediction, i.e., whether by using original body measurements or principal component scores.

 

Material and Methods

 

This study was conducted in the Illpa Experimental Centre of the National University of Altiplano, in Puno Department, Peru. The climate of study area is rainy during summer and dry in winter. It has average annual precipitation of 654.20 mm, with an average annual temperature of 8ºC and average relative humidity of 53.5%. The animals were grazed on natural pastures. The dominating grass species in these areas are Festuca dolichophylla, Muhlenbergia fastigiata, Alchemilla pinnata, Calamagrostis vicunarum and Stipa ichu. Oat hay was supplemented ad libitum. Since birth records were not available, the age of a ewe was estimated by counting permanent incisors as described by Gatenby (1991).

 

Live weights and body measurements were recorded on 100 Corriedale female sheep between 1.5 and 2 years old. Both measurements were taken after eight hours of feed restriction in order to avoid any kind of error due to gut fill. Live A digital weighing scale that could measure to the nearest 0.1 kg was used to record live weight, whereas body measurements were carried out by two technicians by using tape measure and Vernier caliper. The 14 body measurements were: wither height (WH), rump height (RH), thoracic perimeter (TP), abdominal perimeter (AP), fore-shank length (FSL), fore-shank width (FSW), fore-shank perimeter (FSP), tail width (TW), tail perimeter (TPe), hip width (HW), loin width (LWi), shoulder width (SW), forelimb length (FL), and body length (BL).

 

Statistical analyses

The data were organized and analyzed by using several statistical procedures (PROC) in SAS (SAS Inst. Inc., Cary. NC. 2003). Pearson’s correlation coefficients between body measurements and body weights were calculated using the PROC CORR and tested for significance. PCA was performed on body traits measures using PROC FACTOR. PCA was used in order to check whether body traits could be reduced to uncorrelated dimensions, that is, linear combinations of original variables, called as principal components (PC). As a prior to performing PCA, the Kaiser–Guttman rule was used to determine the number of extracted factors, i.e., factors with eigenvalues higher than 1 (Kaiser, 1960). Bartlett’s test of sphericity was used to verify if the correlation matrix was an identity or a sparse one. Kaiser–Meyer–Olkin measures of sampling adequacy of the correlation matrix and communality were also computed to validate the use PCA (sampling adequacy > 0.5). Subsequently, the varimax rotation algorithm was applied to enhance the PC interpretability. Loadings, i.e., estimated values for each body measurement in every PC, higher or equal than 0.50 were used for PCA interpretation.

 

To predict live weights from original body measurements [1], and from established principal component scores [2], a multiple regression analysis was performed by the PROC REG using the stepwise selection procedure. The following regression models were used:

 

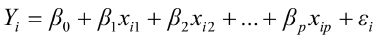, for i = 1,2,3,…,n [1]

 

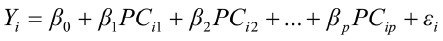, for i = 1,2,3,…,n [2]

 

where 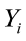is the value of the ith observation; 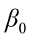is the intercept; 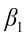, ,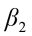…, 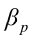are the pth partial regression coefficients; 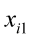, ,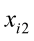…, 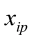and 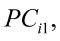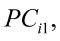…, 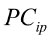are the pth original body measurements and principal component scores, respectively, for the ith observation; 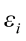is the residual error, assumed as statistically independent, with common mean 0 and variance 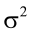, and are approximately normal in distribution.

 

The stepwise procedure provides the best prediction equations for body weight and did not include variables with a P > 0.05 as suggested by Diaz et al. (2004) and Marshall et al. (2005). Accuracies of prediction equations were estimated through the coefficients of multiple determinations (R2) and root mean squared error (RMSE). Akaike’s information criterion (AIC) and Bayesian information criterion (BIC) statistics were also used to assess the quality of the models (goodness of fit and model complexity). The best fit model should have lowest AIC (Akaike, 1974) and BIC values (Schwarz, 1978), maximum R2, and minimum RMSE.

 

Results and Discussion

 

Descriptive analysis of live weight and body measurements

Descriptive statistics of live weight and body measurements are presented in Table 1. There was a greater phenotypic variability among animals for LW, FSW, TW and TPe with coefficients of variation (CV) ranging from 13.62 to 18.08%, whereas the others traits showed smaller variability (CV < 9%). The average LW was 34.4 ± 4.7 kg. The WH (59.8 cm) and RH (61.1 cm) were of average proportion. The average of TP was 82.6 whereas for AP was 96.7 cm. The region of the fore-shank had measures of 20.4 cm in length, 2.5 cm in width, and 8.4 cm in perimeter, whereas BL was 95.5 cm on average. The availability of such information is essential to seek for optimal production efficiency and better value for its products.

 

Pearson’s coefficients of correlation

Pearson’s coefficients of correlation (r) obtained between live weight and body measurements, and among body measurements are presented in Table 2. All the body measurements were positively and significantly (r = 0.20 - 0.78; P < 0.05/0.01) correlated with LW, except FSW (r = 0.18, P > 0.05). LW had the highest correlation coefficient (r= 0.78; P <0.01) with AP, followed by TP (r = 0.64) and BL (r = 0.52). The correlation between AP and TP was also high (r=0.772, P<0.01). On the other hand, the lowest values were observed between LW and TPe (r = 0.20), and between LW and FSW (r = 0.18; P > 0.05). Among the body measurements, strongest correlations were verified between WH and RH (r = 0.93; P < 0.01), and between TW and TPe (r = 0.80; P < 0.01), whereas TW with AP and FSL had relatively low values (r = 0.20; P < 0.05). Our results corroborate with those reported by Afolayan et al. (2006), Sowande and Sobola (2008), for Yankasa, West African dwarf and Karayaka breeds, respectively.

 

Heavier animals tend to have bigger thoracic and abdominal perimeters, indicating that the search for a deep and wide sheep would lead to ewes with more body weight. This can be confirmed by the Pearson’s correlations in Table 2, which were the higher among body weight and body measurements. On the other hand, animals with higher width fore-shank, higher width, and perimeter of the tail, are either unrelated or have a weak relationship (below 0.25), that would not be recommend as prediction variables for the body weight. Among the variables that presented r between 0.26 and 0.52, have better potential to apply in the practice are the hip width and body length, that present r, respectively, 0.500 and 0.517 and can be measure with relatively easy in the handling chute. Therefore, the thoracic and abdominal perimeters, together hip width, and body length, present a good relationship and is of easy of application in the management in the sheep facilities.

 

In Harnali sheep, Kumar et al. (2017), described correlations between body weight and thoracic perimeter, abdominal perimeter, and body length, respectively, form 0.59, 0.44 and 0.32. For females Cornigliese sheep breed, Sabbioni et al. (2020), found correlations from 0.95, 0.86 and 0.89 between body weight and thoracic perimeter, body length and hip width, respectivaly. Sun et al. (2020), in Jamuna Basin sheep, found correlations of the 0.65 between body weight and thoracic perimeter and 0.57 between body weight and body length. Rather et al. (2021) found better correlations of the thoracic perimeter (0.54), abdominal perimeter (0.54) and body length (0.48) with the body weight for Kashmir Merino sheep.

 

Principal component analysis (PCA)

The sampling adequacy Kaiser-Meyer-Olkin statistician was high for Corriedale ewes (0.70), which supports the use of the correlation matrix for PCA, i.e., it indicates that

 

Table 1: Descriptive statistics of live weight (kg) and body measurements (cm) of Corriedale ewes.

 

Body traits	Mean		SD		Minimum		Maximum		CV(%)
LW	34.39		4.68		22		46		13.62
WH	59.80		2.68		50		66		4.49
RH	61.08		2.66		52		68		4.35
TP	82.55		4.40		72		99		5.33
AP	96.96		5.57		80		112		5.74
FSL	20.41		1.25		17		25.5		6.14
FSW	2.51		0.34		2		3		13.75
FSP	8.43		0.59		6		10		7.05
TW	3.17		0.52		2.5		5		16.36
TPe	7.45		1.35		6		17		18.08
HW	19.38		1.60		11		23		8.24
LWi	12.46		1.01		10		18		8.12
SW	19.33		1.44		15		23		7.46
FL	37.06		2.41		27		42		6.51
BL	95.48		4.28		83		104		4.48

SD: standard deviation; CV: coefficients of variation; LW: live weight; WH: wither height; RH: rump height; TP: thoracic perimeter; AP: abdominal perimeter; FSL: fore-shank length; FSW: fore-shank width; FSP: fore-shank perimeter; TW: tail width; TPe: tail perimeter; HW: hip width; LWi: loin width; SW: shoulder width; FL: forelimb length and BL: body length.

 

Table 2: Pearson correlation coefficients among live weight and body measurements in Corriedale ewes.

 

Traits

WH

RH

TP

AP

FSL

FSW

FSP

TW

TPe

HW

LWi

SW

FL

BL

LW

0. 330**

0. 398**

0. 637**

0. 776**

0. 482**

0. 177ns

0.260**

0. 225*

0.200*

0.500**

0.497**

0.514**

0.299**

0.517**

WH

0. 932**

0. 185ns

0. 229*

0. 337**

0. 452**

0.195ns

0. 126ns

-0.007ns

0.316**

0.093ns

0.076ns

0.387**

0.287**

RH

0. 216*

0. 274**

0. 369**

0. 479**

0.211*

0. 225*

0.065ns

0.339**

0.123ns

0.114ns

0.407**

0.359**

TP

0. 772**

0. 271**

0. 161ns

0.138ns

0. 224*

0.162ns

0.383**

0.393**

0.405**

0.177ns

0.356**

AP

0. 314**

0. 192ns

0.168ns

0. 202*

0.137ns

0.447**

0.370**

0.417**

0.270**

0.324**

FSL

0. 112ns

0.259**

0. 202*

0.094ns

0.238*

0.272**

0.156ns

0.378**

0.378**

FSW

0.495**

0. 052ns

0.017ns

0.355**

-0.050ns

0.291**

0.334**

0.242*

FSP

0. 038ns

0.011ns

0.281**

0.083ns

0.280**

0.245*

0.150ns

TW

0.803**

0.034ns

0.394**

0.231*

0.160ns

0.098ns

TPe

-0.229ns

0.638**

0.225*

0.083ns

0.103ns

HW

0.011ns

0.608**

0.219*

0.247*

LWi

0.386**

0.137ns

0.290**

SW

0.208*

0.213*

FL

0.283**

LW: live weight; WH: wither height; RH: rump height; TP: thoracic perimeter; AP: abdominal perimeter; FSL: fore-shank length; FSW: fore-shank width; FSP: fore-shank perimeter; TW: tail width; TPe: tail perimeter; HW: hip width; LWi: loin width; SW: shoulder width; FL: forelimb length and BL: body length. nscorrelation is not significant; *correlation is significant at the 0.05 level (0.20-0.25); **correlation is significant at the 0.01 level (0.259-0.932).

 

 

true PC factors exist (Yakubu et al., 2011). In addition, the Bartlett’s sphericity test showed a chi-square highly significant (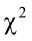 = 925.06; P < 0.001) which also supports the use of PCA.

 

The estimated factor loadings extracted by PCA, eigenvalues and variation explained by each factor, are presented in Table 3. After a varimax rotation of the component matrix, only four PC were extracted with eigenvalues equal to or higher than one. The extraction of only four PC allows us to better understand the complex correlations among traits, as well as the use of more parsimonious models (Mota et al., 2016). Legarra et al. (2004) reported that more parsimonious models require smaller computational demands and are less susceptible to numerical errors. In other words, fewer PC are generally enough to explain a great part of all variability (Boligon et al., 2013).

 

The four PC contributed for 68.7% of the total variation among all traits. From the total variance, 33.67% was accounted by the first component (PC1). PC1 had high positive loadings for LW, TP, AP, HW, and SW. The second component (PC2) explained 15.39% of the total variance and was characterised by high positive loadings for WH, RH, FSL and FL. The third component (PC3) which was associated with TW, TPe and LWi, accounted for 11.39% of the total variance, whereas the fourth component (PC4) had high positive loadings for FSW, FSP and SW, and contributed to 8.26% of the total variance. In addition, communalities represent the proportion of the variance in the original variables that is accounted by the PC. In general, the communalities were high for almost all traits, ranging from 0.39 (FL) to 0.95 (TPe) in Corriedale ewes (Table 3). The use of four PC may play a crucial role in the ranking of animals. This provides a chance to better select animals by using groups of traits instead of a single trait itself (Yakubu et al., 2011; Pinto et al. 2006).

 

Silva et al. (2015), by using a ranking method in performance testing in Morada Nova sheep population, reported that the three first PC better explained the most variability of all evaluated traits. In a Portuguese Bordaleira sheep population, Cerqueira et al. (2011) observed that the two PC were enough to explain 70.5% of the total variation, and PC1 explained 61.4% itself. These authors reported that body measurements of height at withers, height at back, height at rump, length of trunk, length of head, perimeter of the shin and live weight contributed positively for most of variation. Mavule et al. (2013) studying two Zulu sheep populations (young and adult) reported that two PC for a young and four PC for an adult population were sufficient to explain most of the variability. Is clear that variability of body measurements might be different across breeds, but some traits commonly influence sheep populations no matter the breed. This is an indicative that these traits could integrate a selection index in breeding programs for different sheep breeds.

 

Figure 1 showed the component plot of the first three PC in rotated space for body measurements. The plot clearly showed that the body measurements have been clustered into the following five groups: 1- by TW and TPe; 2- by LWi and SW; 3- by LW, TP and AP; 4- by FSL, HW and BL; 5- by FL, FSP, FSW, WH and RH.

 

 

Predictions of live weight of Corriedale ewes from body measurements and their principal component scores

Table 4 shows the regression equations predicting LW of Corriedale ewes from original body measurements and their PC scores. Results of the stepwise multiple regression analysis revealed that abdominal perimeter alone accounted for 60% of the variation in live weight. The inclusion of body length increased this proportion up to 68%. The accuracy of the model was further improved to 76% when shoulder width, fore-shank length and loin width were added to the equation. Besides the higher R2, this model showed lowest AIC, BIC and RMSE values, which confirms its better goodness of fit when compared to the models that use original body measurements. Kunene et al.(2009)

 

Table 3: Eigenvalues and factor loading (PCs) after varimax rotation and communality of live weight and body measurements of Corriedale ewes.

Body traits	PC1	PC2	PC3	PC4	Communality
LW	0.84	0.30	0.16	0.14	0.83
WH	0.06	0.89	-0.02	0.18	0.82
RH	0.10	0.90	0.05	0.20	0.86
TP	0.81	0.09	0.13	0.08	0.69
AP	0.84	0.15	0.09	0.12	0.76
FSL	0.39	0.53	0.12	-0.04	0.44
FSW	-0.03	0.41	-0.02	0.74	0.72
FSP	0.06	0.16	0.04	0.72	0.54
TW	0.06	0.15	0.85	0.09	0.75
TPe	0.03	0.01	0.97	0.00	0.95
HW	0.54	0.14	-0.26	0.56	0.70
LWi	0.46	0.05	0.68	-0.07	0.68
SW	0.54	-0.14	0.23	0.61	0.74
FL	0.15	0.55	0.11	0.25	0.39
BL	0.48	0.45	0.06	-0.02	0.43
Eigenvalues	5.05	2.31	1.71	1.24
% of total variance	33.67	15.39	11.39	8.26
Cumulative variance (%)	33.67	49.06	60.45	68.71

Values in bold are ≥0.5; measure of sampling adequacy = 0.698. LW: live weight; WH: wither height; RH: rump height; TP: thoracic perimeter; AP: abdominal perimeter; FSL: fore-shank length; FSW: fore-shank width; FSP: fore-shank perimeter; TW: tail width; TPe: tail perimeter; HW: hip width; LWi: loin width; SW: shoulder width; FL: forelimb length and BL: body length.

 

Table 4: Stepwise multiple regression equations for predicting live weight from original body measurements and their principal component scores and its respective coefficients of determination (R2), root mean square error (RMSE), Akaike’s information criterion (AIC) and Bayesian information criterion (BIC) of Corriedale ewes.

Model	Predictors	Models	R2	RMSE	AIC	BIC
Original body measurements as predictors
1	AP	LW= -28.933 + 0.653AP	0.60	2.9680	219.5587	219.7488
2	AP, BL	LW= -52.041 + 0.572AP + 0.324BL	0.68	2.6727	199.5749	200.1044
3	AP, BL, SW	LW= -56.542 + 0.505AP + 0.305BL + 0.665SW	0.72	2.5377	190.1671	191.0550
4	AP, BL, SW, FSL	LW= -61.622 + 0.471AP + 0.240BL + 0.664SW + 0.716FSL	0.75	2.4127	181.0219	182.6954
5	AP, BL, SW, FSL, LWi	LW= -62.057 + 0.452AP + 0.222BL + 0.557SW + 0.658FSL + 0.578LWi	0.76	2.3684	178.2539	180.4312
Principal components as predictors
1	PC1	LW= 34.390 + 3.924PC1	0.70	2.6591	197.5749	197.3420
2	PC1, PC2	LW= 34.390 + 3.924PC1 + 1.385PC2	0.79	2.5246	188.1671	187.5310
3	PC1, PC2, PC3	LW= 34.390 + 3.924PC1 + 1.385PC2 + 0.757PC3	0.82	2.4001	179.0219	178.2860
4	PC1, PC2, PC3, PC4	LW= 34.390 + 3.924PC1 + 1.385PC2 + 0.757PC3 + 0.651PC4	0.83	1.9436	137.7839	140.3047

LW: live weight; AP: abdominal perimeter; FSL: fore-shank length; LWi: loin width; SW: shoulder width and BL: body length.

 

reported that linear regression coefficients of heart girth and wither height could be used to estimate the body weight of the Zulu sheep with R2 of 0.66 to 0.49, respectively. In the Anatolian Peninsula, the study of Yilmaz et al. (2013) reported that the model considered all traits (rump height, withers height, back height, chest depth, chest width and body length) presented the best R2 = 0.76 to estimate mature live weight in a Karya sheep population.

 

However, better results were achieved when using PC instead of original body measurements (Table 4). As mentioned above, four PC contributed for 68.7% of the total variation between recorded body traits. Hence, we performed a stepwise multiple regression analysis using one, two, three and four PC (4 models). It was observed that goodness of fit increased by including the four PC in the model. Although the use of more parsimonious models are preferable as aforementioned, the model considering 4 PC have lowest RMSE, AIC and BIC values and highest R2 (Table 4). Nevertheless, the 4 PC model are more parsimonious than the model using five original measurements, the best fit model among models using original measurements. In a similar study, Yadav et al. (2016) have founded that body weight prediction model with PC1 and PC2 presented better R2 (0.94) and lowest RMSE (1.86) rather the model with only PC1 (R2 = 0.80 and RMSE=3.84) in a Madgyal sheep population. The PC obtained here may be used as a group of variables or even in a selection index. In this case, the selection index would have four weighted coefficients which will decrease computational demands (Pinto et al., 2006; Mota et al., 2016).

 

From these results, we can suggest that it is possible to predict live weight of Corriedale ewes by using body measurements, which is an advantage for farmers who cannot afford a weighing scale. In addition, prediction of live weight using four PC calculated from the body measurements is rather better alternative than using original measurements. The four PC reported here have high association with the most evaluated body measurements.

 

Conclusions

 

Our results suggested that principal components analysis is a suitable approach to evaluate live weight and the relationship between body measurements of Corriedale sheep population in Peru. This approach allows us to predict animals live weight through regression equations using principal components scores. Using this approach also represents a viable alternative for the farmer to rank their animals.

 

Conflict of interest

 

There were no conflicts of interest.

 

Acknowledgements

 

The authors are grateful for valuable assistance of all staff of Illpa Experimental Centre from the National University of Altiplano.

 

authors contribution

 

Ali William Canaza-Cayo; Investigation, Data analysis, Formal analysis. Ali William Canaza-Cayo, Rodrigo Reis Mota, Fernando Amarilho-Silveira; Statistical analysis, Methodology, Writing of Original draft. Darlene Ana Souza Duarte, Jaime Araujo Cobuci; Editing, Review.

 

References

 

• Afolayan RA, Adeyinka IA, Lakpini CAM (2006). The estimation of live weight from body measurements in Yankasa sheep. Czech J. Anim. Sci. 51: 343–348. https://doi.org/10.17221/3948-CJAS

• Akaike H (1974). Akaike A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19: 716–723. https://doi.org/10.1109/TAC.1974.1100705

• Akinsola OM, Nwagu BI, Orunmuyi M, Iyeghe-Erakpotobor GT, Eze ED, Shoyombo AJ, Okuda EU, Louis U (2014). Prediction of bodyweight from body measurements in rabbits using principal component analysis. Sci. J. Anim. Sci. 3: 15–21.

• Atta M, El khidir OA (2004). Use of heart girth, wither height and scapuloischial length for prediction of liveweight of Nilotic sheep. Small. Rumin. Res. 55: 233–237. https://doi.org/10.1016/j.smallrumres.2004.01.005

• Boligon AA, Bignardi AB, Mercadante MEZ, Lobo RB, Albuquerque LG (2013). Principal components and factor analytic models for birth to mature weights in Nellore cattle. Livest. Sci. 152: 135–142. https://doi.org/10.1016/j.livsci.2013.01.005

• Cerqueira JOL, Feás X, Iglesias A, Pacheco LF, Araújo JPP (2011). Morphological traits in Portuguese Bordaleira de Entre Douro e Minho sheep: divergence of the breed. Anim. Prod. Sci. 51: 635–641. https://doi.org/10.1071/AN10147

• Diaz MT, Cañeque V, Lauzurica S, Velasco S, Ruiz de Huidobro F, Pérez C (2004). Prediction of suckling lamb carcass composition from objective and subjective carcass measurements. Meat Sci. 66: 895–902. https://doi.org/10.1016/j.meatsci.2003.08.013

• Eyduran E, Waheed A, Tariq MM, Iqbal F, Ahmad S (2013). Prediction of live weight from morphological characteristics of commercial goat in Pakistan using factor and principal component scores in multiple linear regression. J. Anim. Plant Sci. 23: 1532–1540.

• Enevoldsen C, Kristensen T (1997). Estimation of body weight from body size measurements and body condition scores in dairy cows. J. Dairy Sci. 80: 1988–1995. https://doi.org/10.3168/jds.S0022-0302(97)76142-3

• Gatenby RM (1991). Sheep. The tropical agriculturalist Series, CTA, MacMillan, London, pp. 6–10.

• Iñiguez L (2011). The challenges of research and development of small ruminant production in dry areas. Small. Rumin. Res. 98(1-3): 12-20. https://doi.org/10.1016/j.smallrumres.2011.03.010

• Instituto Nacional de Estadística e Informática - INEI (2012). IV Censo Nacional Agropecuario 2012. [Internet]. Disponible en: http://proyectos.inei.gob.pe/web/DocumentosPublicos/ResultadosFinalesIVCENAGRO.pdf (accessed 04.07.19).

• Jolliffe IT (2002). Principal Component Analysis. Springer, 2nd ed., New York.

• Kaiser HF (1960). The application of electronic computers to factor analysis. Educ. Psychol. Meas. 20: 141–151. https://doi.org/10.1177/001316446002000116

• Kumar S, Dahiya SP, Malik ZS, Patil CS (2017). Prediction of body weight from linear body measurements in sheep. Indian J. Anim. Res. 1-4. https://doi.org/10.18805/ijar.B-3360

• Kunene NW, Nesamvuni AE, Nsahlai IV (2009). Determination of prediction equations for estimating body weight of Zulu (Nguni) sheep. Small. Rumin. Res. 84: 41–46. https://doi.org/10.1016/j.smallrumres.2009.05.003

• Legarra A, Misztal I, Bertrand JK (2004). Constructing covariance functions for random regression models for growth in Gelbvieh beef cattle. J. Anim. Sci. 82: 1564–1571. https://doi.org/10.2527/2004.8261564x

• Legaz E, Cervantes I, Pérez-Cabal MA, Fuente LF, Mártinez R, Goyache F, Gutiérrez JP (2011). Multivariate characterisation of morphological traits in Assaf (Assaf.E) sheep. Small. Rumin. Res. 100: 122–130. https://doi.org/10.1016/j.smallrumres.2011.06.005

• Marshall W, Collantes M, Corchado A, Bertot JA, Uña F, Torres V, Sarduy L (2005). Prediction of the carcass. tissue composition and regional traits in Pelibuey sheep supplemented with poultry litter and soybean meal. Cuban J. Agr. Sci. 39: 33–40.

• Mavule BS, Muchenje V, Bezuidenhout CC, Kunene NW (2013). Morphological structure of Zulu sheep based on principal component analysis of body measurements. Small. Rumin. Res. 111: 23–30. https://doi.org/10.1016/j.smallrumres.2012.09.008

• Mota RR, Costa EV, Lopes PS, Nascimento M, Silva LP, Silva FF, Marques LFA (2016). Multi-Trait analysis of growth traits: fitting reduced rank models using principal components for Simmental beef cattle. Cienc. Rural. 46: 1656–1661. https://doi.org/10.1590/0103-8478cr20150927

• Pinto LFB., Packer IU, DE Melo CMR, Ledur MC, Coutinho LL (2006). Principal components analysis applied to performance and carcass traits in the chicken. Anim. Res. 55: 419–425. https://doi.org/10.1051/animres:2006022

• Rather MA, Bashir I, Hamdani A, Khan NN, Ahangar AA, Nazki M (2021). Prediction of body weight from linear body measurements in Kashmir Merino Sheep. Adv. Anim. Vet. Sci. 9: 189-193. https://doi.org/10.17582/journal.aavs/2021/9.2.189.193

• Riva J, Rizzi R, Marelli S, Cavalchini LG (2004). Body measurements in Bergamasca sheep. Small. Rumin. Res. 55: 221–227. https://doi.org/10.1016/j.smallrumres.2003.12.010

• Sabbioni A, Beretti V, Superchi P, Ablondi M (2020). Body weight estimation from body measures in Cornigliese sheep breed. Ital. J. Anim. Sci. 19: 25-30. https://doi.org/10.1080/1828051X.2019.1689189

• SAS Institute Inc (2003). SAS User’s Guide: Version 9.1. SAS Institute Inc.,Cary, NC.

• Schwarz G (1978). Estimating the dimension of a model. Ann. Stat. 461–464. https://doi.org/10.1214/aos/1176344136

• Silva DC, Azevêdo DMMR, Alves AA, Campelo JEG, Oliveira ME, Malhado CHM (2006). Estimativa do peso vivo através do perímetro torácico de ovinos Santa Inês. Ver. Cient. Prod. Anim. 8: 41–46.

• Silva MC, Lopes FB, Vaz CMS, Paulini F, Montesinos IS, Fioravanti MCS, McManus C, Sereno JRB (2013). Morphometric traits in Crioula Lanada ewes in Southern Brazil. Small. Rumin. Res. 110: 15–19. https://doi.org/10.1016/j.smallrumres.2012.09.002

• Silva MS, Shiotsuki L, Lôbo RNB, Facó O (2015). Principal component analysis for evaluating a ranking method used in the performance testing in sheep of Morada Nova breed. Semin. Cienc. Agrar. 36: 3909–3922. https://doi.org/10.5433/1679-0359.2015v36n6p3909

• Sowande OS, Sobola OS (2008). Body measurements of west African dwarf sheep as parameters for estimation of live weight. Trop. Anim. Health Prod. 40: 433–439. https://doi.org/10.1007/s11250-007-9116-z

• Sun MA, Hossan MA, Islam T, Rahman MM, Hossain MM, Hashem MA (2020). Different body measurement and body weight prediction of Jamuna Basin sheep in Bangladesh. SAARC J. Agric. 18: 183-196. https://doi.org/10.3329/sja.v18i1.48392

• Williams GW, Anderson DP (2020). The Latin American Livestock Industry: Growth and Challenges. Choices, 34(316-2020-617): 1-11.

• Yadav DK, Arora R, Jain A (2016). Principal component analysis of body measurements based morphological structure of Madgyal sheep. Indian J. Anim. Sci. 86: 568–571.

• Yakubu A, Ayoade JA (2009). Application of principal component factor analysis in quantifying size and morphological indices of domestic rabbits. Int. J. Morphol. 27: 1013–1017. https://doi.org/10.4067/S0717-95022009000400009

• Yakubu A, Salako AE, Imumorin IG (2011). Comparative multivariate analysis of biometric traits of West African Dwarf and Red Sokoto goats. Trop. Anim. Health Prod. 43: 561–566. https://doi.org/10.1007/s11250-010-9731-y

• Yilmaz O, Cemal I, Karaca O (2013). Estimation of mature live weight using some body measurements in Karya sheep. Trop. Anim. Health Prod. 45: 397–403. https://doi.org/10.1007/s11250-012-0229-7